I was recently trying to do some of my own search indexing on webpages. The first obstacle in this was identifying what content on the page is of interest and what is not. A typical website presents not only some content but also the entire brand of the website. This is true for websites like the New York Post or Reddit. The HTML of a website is generally parsed as a tree structure. So the problem I am looking to solve is identifying the point in the tree below which all the content resides.

Approaching this problem

I initially came up with a few ideas

1. Use published standards like the <article> tag.
2. Develop a profile for each website I wanted to index
3. Develop a machine learning model that relies on some form of training data.
4. Develop a heuristic model based on assumptions of the structure

The first option was ruled out because no one really follows the standards. The second option was ruled out because it would be too time consuming to get right and websites are always being updated.

The idea of developing a machine learning model was very appealing, but not something I have experience with. I came up with two theoretical sources of training data. The first was to run the model and display the results to a human to develop a training dataset. Each point in the dataset would be binary, answering the question "Did the algorithm satisfactorily identify the content?" My second idea for feedback was to develop some sort of browser plugin that used retina tracking from a webcam to determine what portions of a page a human looks at. For this to work, you would need to combine the retina tracking with the knowledge of what portions of the page were rendered on the screen at the time. I think these were both good ideas but are too large of a project to tackle as an initial attempt at getting this right.

A heuristic model

For a heuristic model to work, I needed to make some assumptions about the structure of the HTML. I started with these assumptions

1. Two non-similar pages on the same website should share some amount of HTML
2. The portion of the HTML that is content should contain a large percentage of the visible HTML
3. The portion of the HTML that is content should not be nested deeply within the tree structure.

There really is no correct answer as to what is content and what is not content on a given webpage. As a result, no algorithm I can write can possibly get the answer correct all the time. It is far more important for the algorithm not to exclude actual content than it is for the algorithm to always exclude non-content.

Removing non-visible HTML

The first place to start is by removing from consideration anything not visible to a user. It is possible to do this by actually rendering the HTML using a tool such as Selenium. This process is always going to be slower than just parsing the HTML. I decided I did not want to render the HTML unless I absolute had to.

For my purposes I settled on the following

1. Ignore the head tag
2. Ignore the script tags
3. Ignore the style tags
4. Ignore HTML comments

This works satisfactorily for me and is very fast. It actually speeds up the process quite a bit, because it removes so much HTML from consideration. Most webpages have many embedded CSS and Javascript tags nowadays.

Weighting each node

After parsing the HTML, we have a tree structure. We have already established that some of this tree structure is not content. We want to traverse the tree structure to identify a particular point in the tree below which the content lies.

At each level in the tree, it must be decided which node is descended upon next. For this decision making, a value is assigned to each node. This value is computed by walking the tree and computing for a node and all its children the length of the text nodes. A text node is something which may be rendered on the page. For example, the HTML <p>Hello from hydrogen18</p> contains a text node of "Hello from hydrogen18". This counts towards the value assigned to that node, whereas the length of the p tags does not. For real world examples, it is also important to remove repeated whitespace from the text. I am unsure why, but many webpages contain large amounts of repeated whitespace.

The tree structure of a webpage can have many nodes, so assigning this value is relatively expensive. Since the tree structure does not change as the algorithm searches through it, the result of the computation can be memoized. This means that even though the heuristic algorithm may run for many iterations, it only has to perform this computation once for any given node.

Choosing the next node

If the algorithm descends, it always descends into the node with the largest percentage of text. This is a typical greedy algorithm. But before this decision is made, two tests are applied.

With a weight chosen for each portion of the subtree, the algorithm can decide which portion of the tree to descend into next. The algorithm must also have some condition that halts descent. If it did not then the algorithm will always land on a leaf node in the tree. For most webpages, this would exclude most of the content.

Since each node now has a weight, we can compute the relative weight for each node. The relative weight is the percentage of text it contains in relation to all other nodes at this level in the tree. This is just a standard percentage calculation. Here is a simple example with 3 nodes

The weights of each node

\( N_1 = 1725, N_2 = 34125, N_3 = 124\)

The relative weight of node 2

\( r(N_2) = \frac{N_2}{\sum_{i=1}^{i=3} N_i} \approx 0.948\)

Since this value is always a percentile, no node can ever have a relative weight equal to 1.0.

The first test is what I call the spread test. This is percentile difference between the smallest and largest relative weight of the nodes. Using our above example, we already know the value \( r(N_2)\). It is the node with the largest weight. Node 3 would have the smallest weight with a value of \( r(N_3) \approx 0.0034\).

This gives a spread of

\( 0.948 - 0.00344 = 0.94456\).

By comparing this value against a configurable value, the algorithm can use it to decide if descent should halt. If this test fails, descent halts. My experimental observation is that the relative spread is usually a very high number, greater than \(0.98\). After descending into the tree, there is a sudden drop in the value.

The next test is the absolute test. This test compares the relative weight of the largest node against a threshold. The threshold is computed as

\( t(d) = 0.001 + ln(1.0 + d/7.0)\)

Where \(d\) is the number of times the algorithm has descended. This value of \(t(d)\) increases as the algorithm descends farther into the tree. Since the relative weight of the largest node is always less than \(1.0\) it also establishes an absolute depth limit to the recursion. In this case when \(d = 13\) the value of \(t(d)\) becomes greater than \(1.0\). I did not choose this formula based on any mathematical principle. I just needed something that increased with depth but not quickly as the depth did. If this test fails, descent halts.

Once descent halts, the node and all of its children are considered to be content.

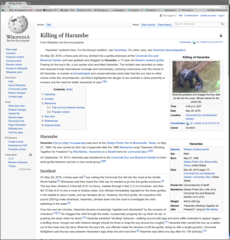
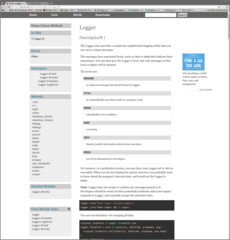
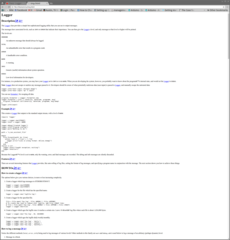
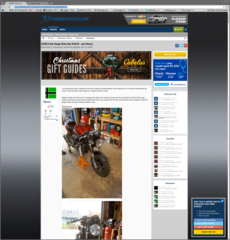
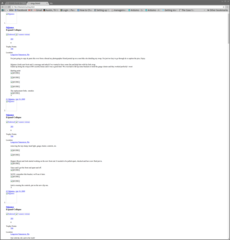
What it looks like in action

To implement the above, I wrote a ruby gem. It is relatively simple, using the "Nokogiri" gem to parse the HTML. I was not expecting great results from this, but it turns out to work pretty well. After the HTML is identified, the CSS is gone so things usually look strange. But the idea of this was to strip out just the content, so I consider that acceptable.

Here are some examples

Getting it for yourself

You can get this gem for yourself on github. The readme contains more information, but here is a basic example, you should use Ruby 2.0 or newer. You will also need the bundler gem installed in order to install directly from GitHub.

$echo -ne "source 'https://rubygems.org'\ngem 'content_finder', git: 'https://github.com/hydrogen18/content_finder.git/'" > Gemfile
$bundle install

...output from bundle install...

$ curl --silent https://aphyr.com/posts/333-serializability-linearizability-and-locality | content_finder 
<div id="content">
<article class="primary post">
  <div class="backdrop">
...more html...

Posssible improvements

There are many possible improvements to the above heuristic algorithm.

For the spread test, instead of comparing against a constant value it is likely possible to detect a large change in the value. When the change is detected, this would halt the descent of the algorithm. It is possible that some form of a Finite impulse response filter could be used to implement this.

There is also the possibility of adding a test that evaluates the fitness of the result. The fitness of the result would be an additional heuristic value. You could compute it by considering the chosen HTML against the excluded HTML. If this test fails, it would be possible to travel back up the tree and try alternate results.